How hash tables outperform other data structures

I guess everyone who’s been in the programming world long enough has heard about this data structure at least once.

Hash tables excel when you need rapid lookups, quick inserts, and fast deletions. But there’s no free lunch in computer science. They come with their own set of trade-offs —which will appear in this article.

So, before you get delighted by the allure of amazing performance, make sure you’re choosing hash tables for the right reasons.

Imagine such story

Vin Diesel is in charge of creating a seat management system for a coworking company. His task is to design a system that tracks seats and the people occupying them:

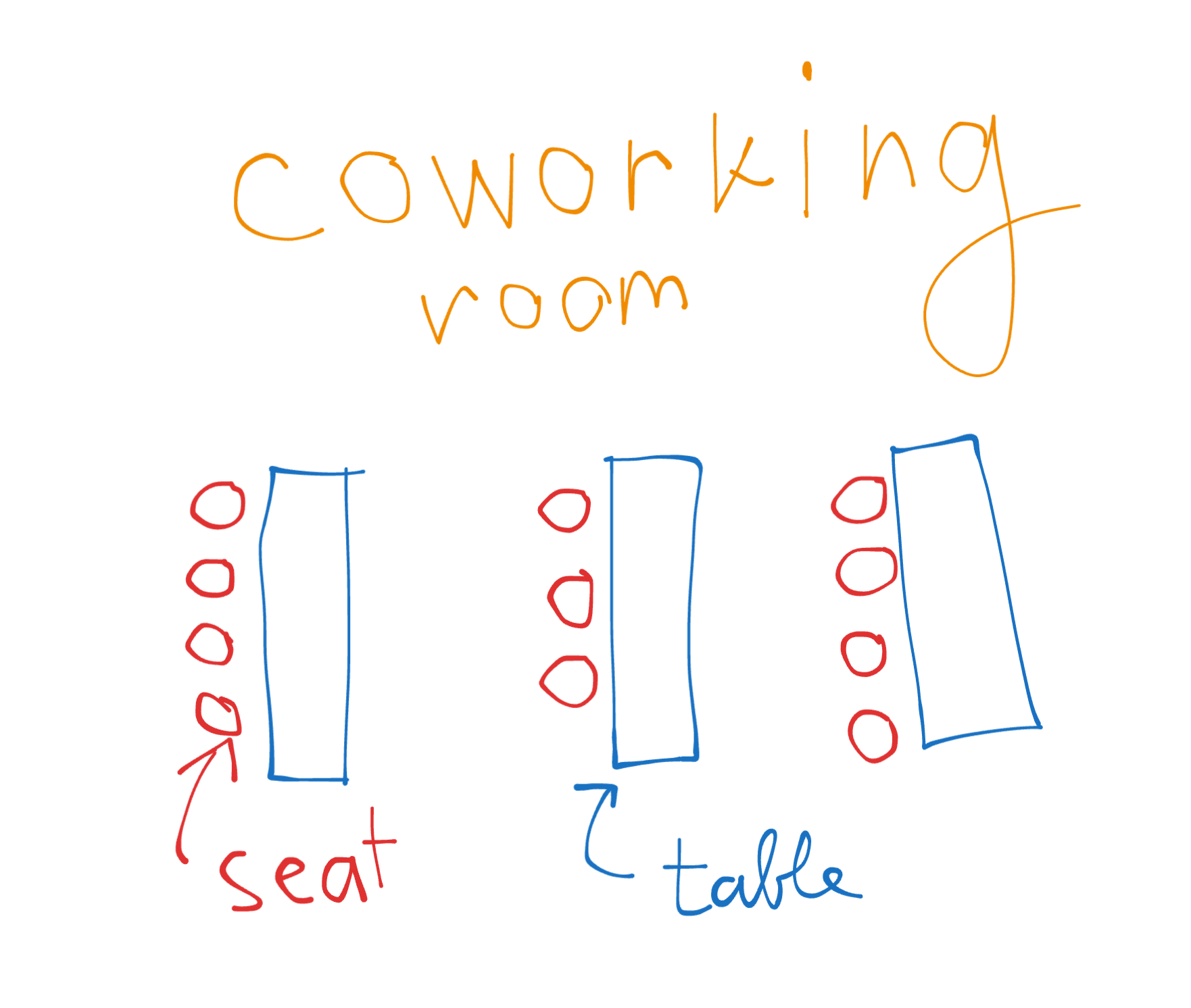
Coworking room illustration

Knowing that, he creates a Room class with methods to manage seats and the people occupying them:

class Seat { 
 id: string
 occupiedById: string 
}

class Room {
  seats: ???? = ???? <---- Choose relevant structure here

  kickPerson(id) {}
  searchPerson(id) {}
  occupyAvailableSeat(id) {}
  addSeat() {}
  removeSeat() {}
}

Now he needs to store somehow those seat objects in memory. Vin knows that the rooms in coworkings are not that big, with a maximum of 10 people. He thought about applying some data structures to store this data:

Array
Linked List
Hash Table

Before deciding, Vin knows he needs to consider the operations he’ll perform and the small amount of data. Which one will he choose?

From a performance perspective, any of these would work just fine. The number of seats is so small that the choice won’t impact performance much. But from a coding perspective, Vin decides to keep it simple and use an array. There’s no need to complicate things with a linked list or hash table, which would add unnecessary complexity.

Great, Vin chose an array! Now he can implement the room methods using this straightforward structure.

For example, when he wants to find someone inside the room, he simply searches through each member and checks if that member is the one he’s looking for. With at most 10 seats, this is quick and easy.

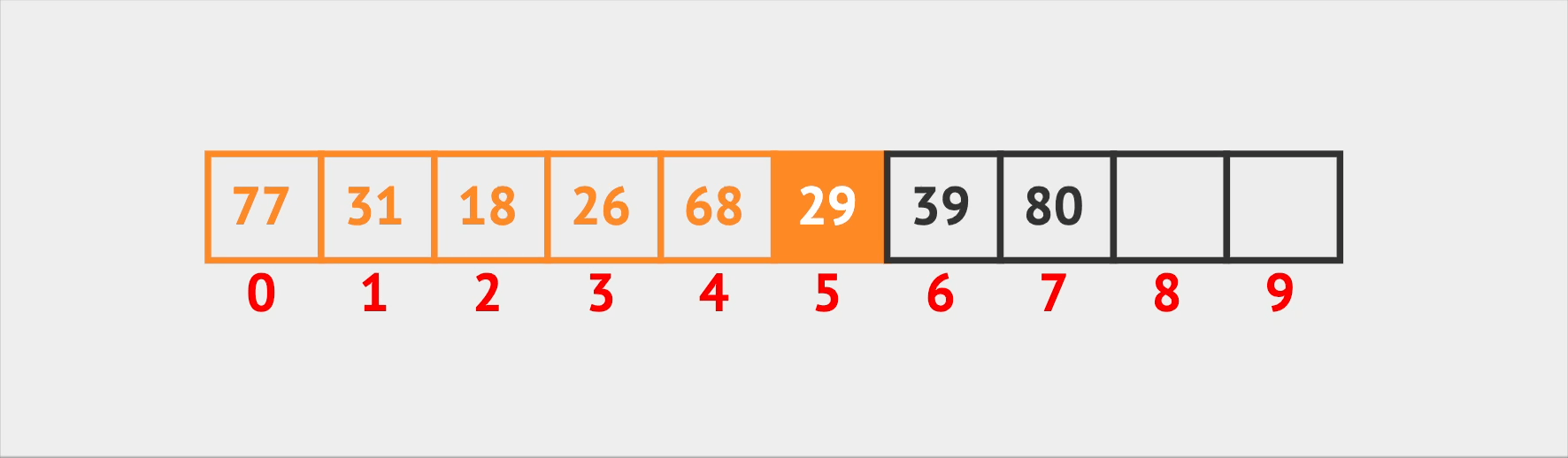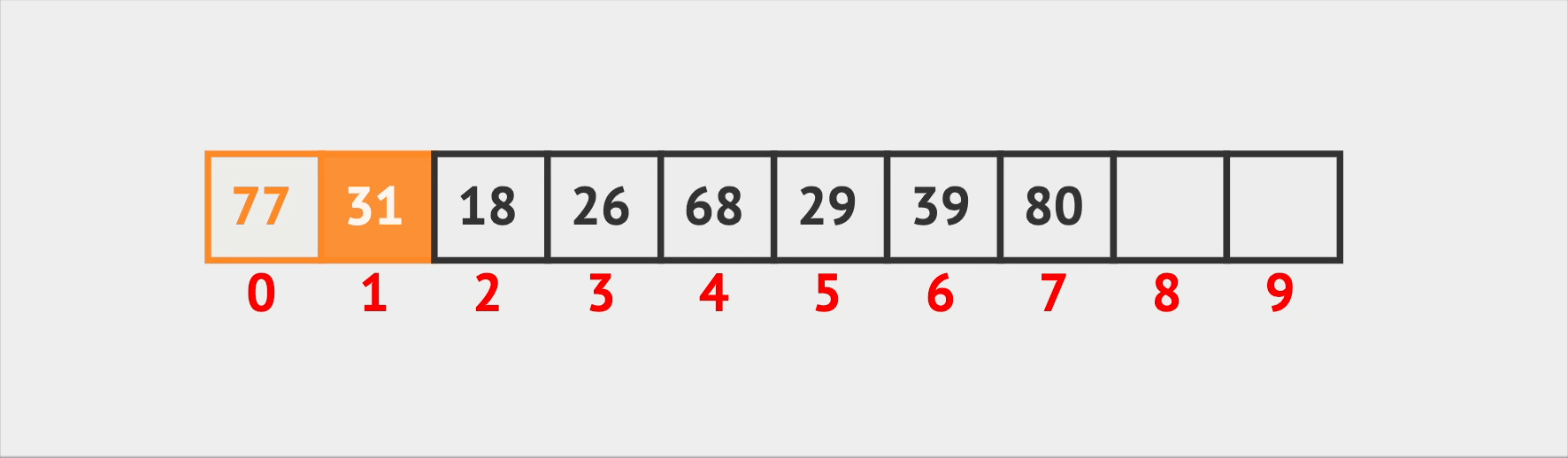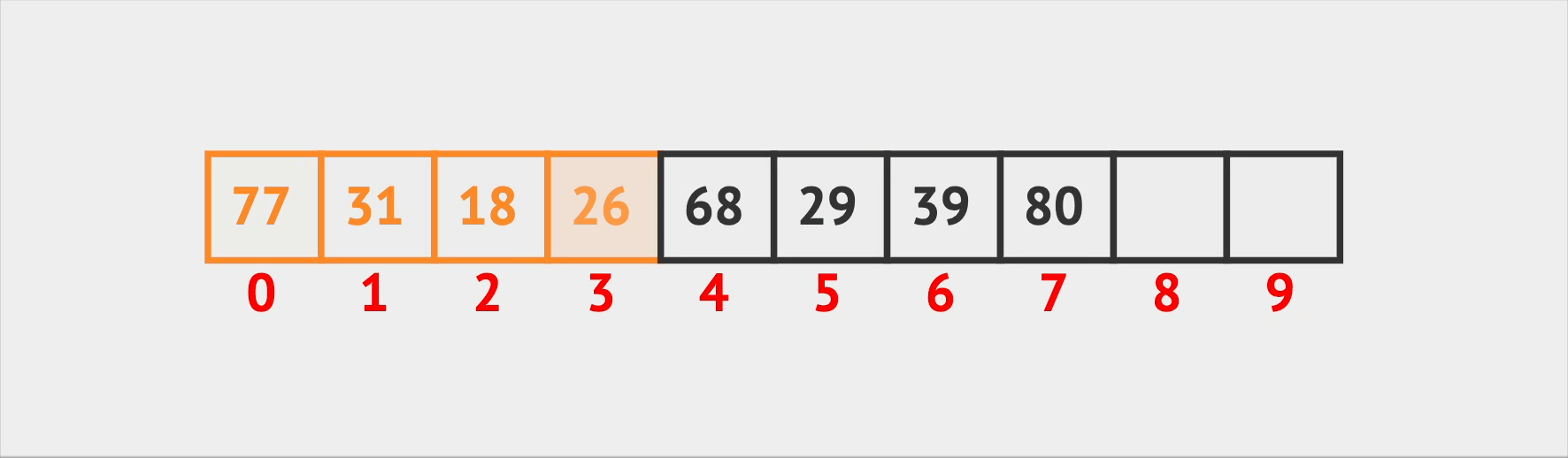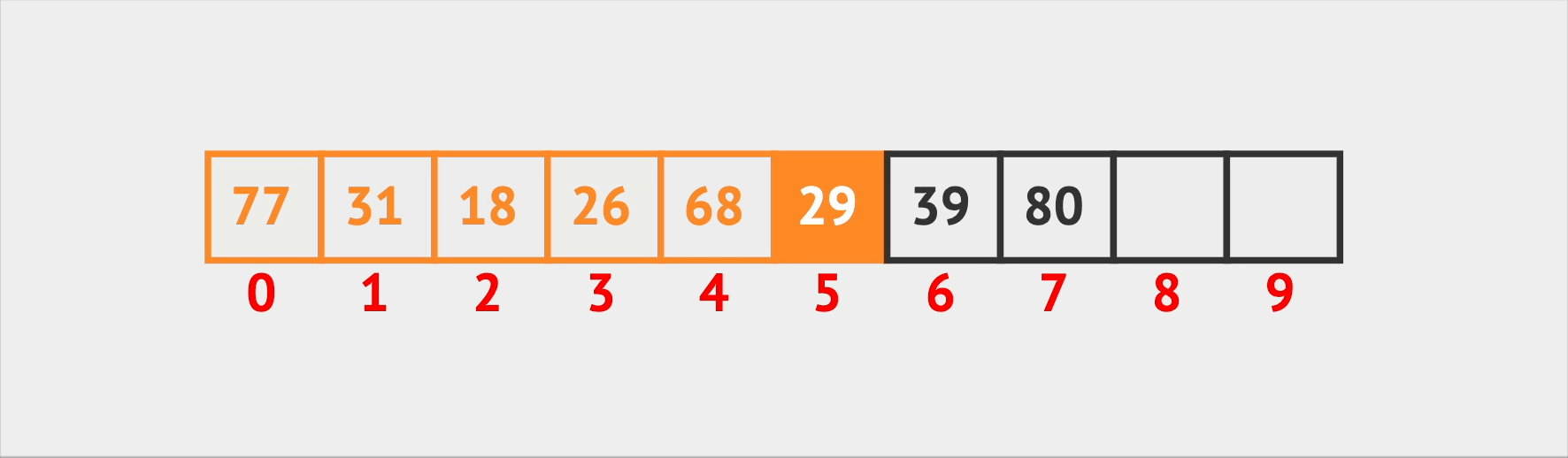
Search Operation (pseudo code):

Iterate through each seat with index:
  If seat.occupiedById === id:
    Return index
Return –1

Almost the same logic goes for the delete operation. When Vin needs to kick someone out of a seat, he first searches for the seat they’re in. After he finds it, he removes the person and then swaps the remaining elements to eliminate any empty spaces in the array. This keeps the seating arrangement tidy and efficient.

Delete Operation (pseudo code):

Iterate through each seat with index:
  If seat.occupiedById === id:
    Remove occupiedById from it
    Return true
Return false

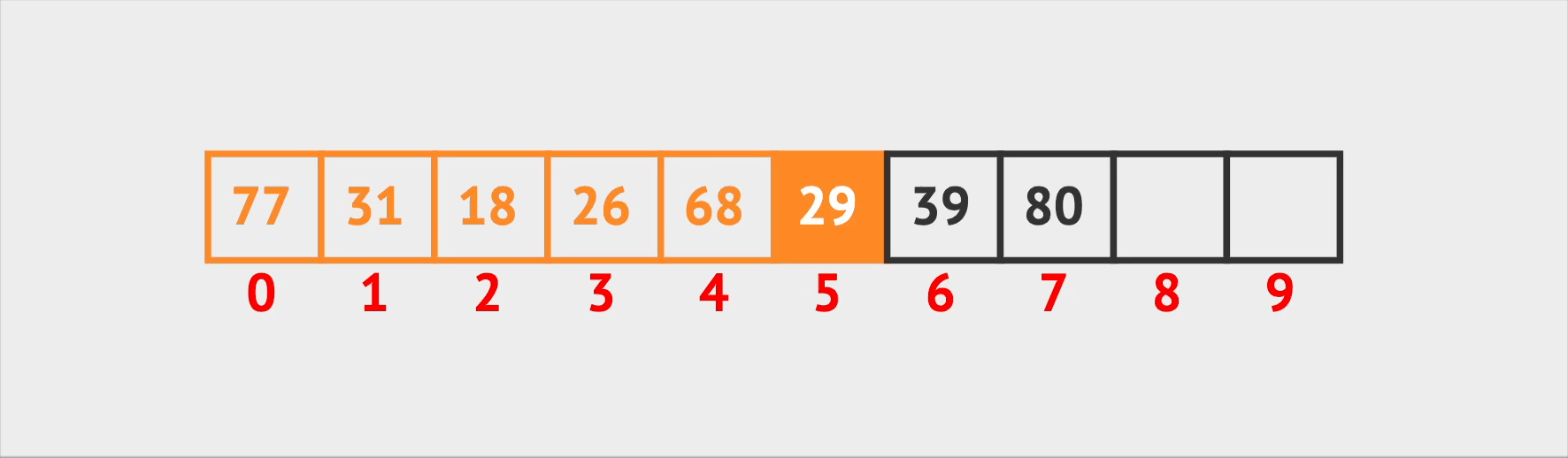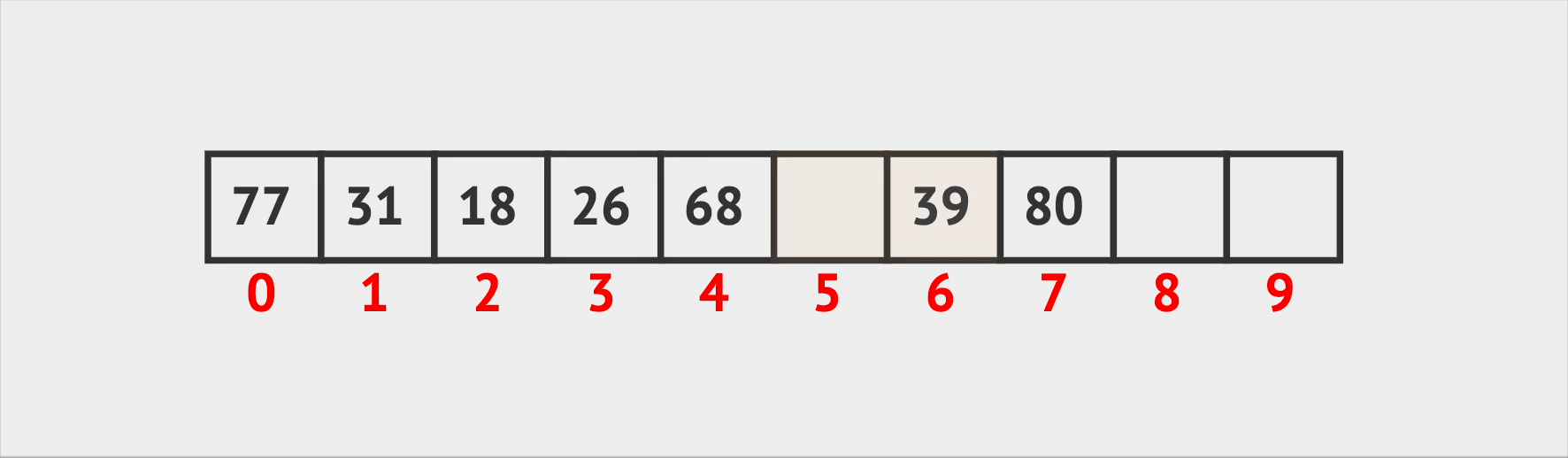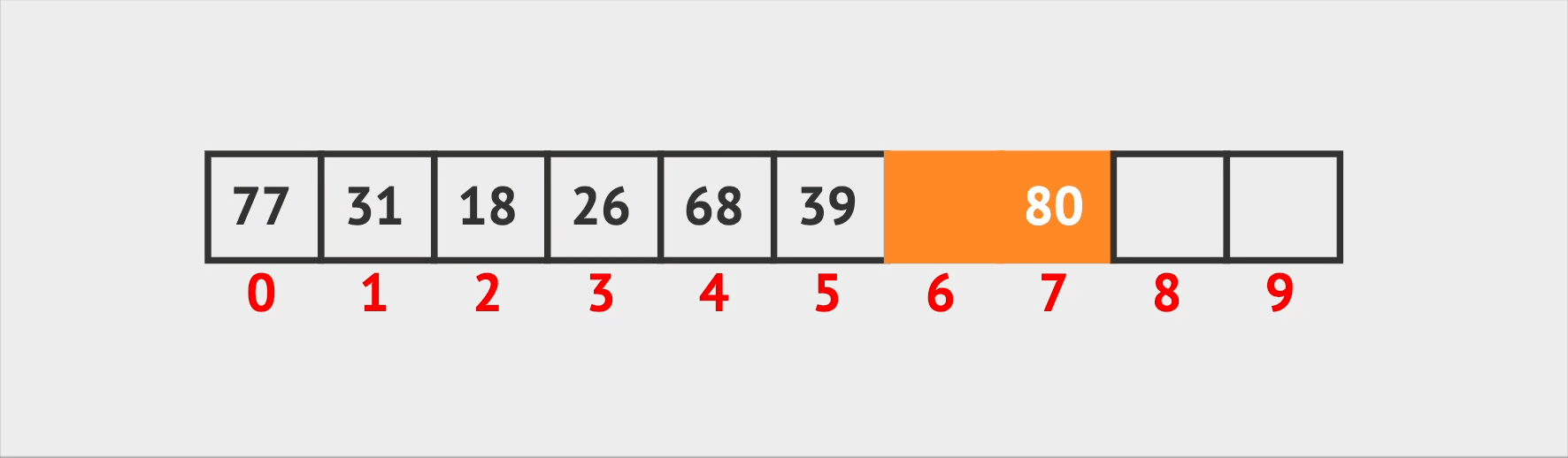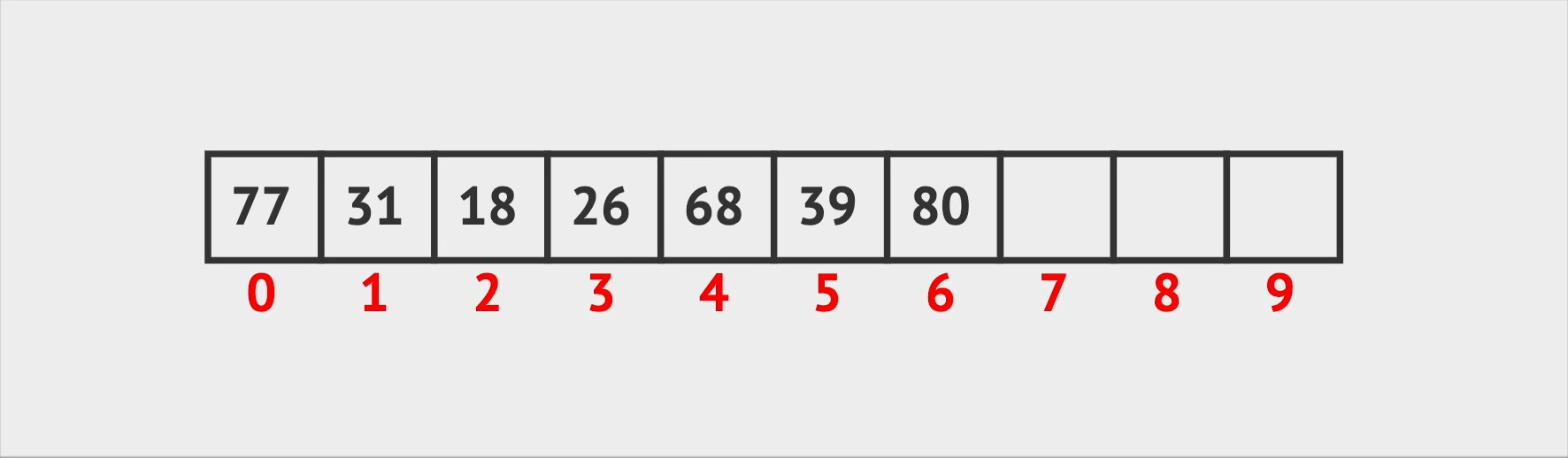
Delete operation GIF

And if Vin wants to add someone, he simply adds the new person to the next available seat. If the room isn’t full, this operation is quick and easy, otherwise, it will take time to find a new room to fill all those people (create a new array with doubled capacity).

Insertion Operation (pseudo code):

Add a new seat with occupiedBy.id = id at the end
Return new index

Insert operation GIF

As you can see, Vin Diesel has created all the methods for the Room class using an array, allowing effective management of seats and people who want to sit there. To perform these operations, at most N steps are needed, where N is the number of seats in the room. Since N is capped at 10, the worst-case scenario involves no more than 10 operations per method.

Nice! The software is working perfectly for the coworking company.

Another story

Now imagine that a ticketing company hires Vin Diesel to implement a class for booking stadium tickets. The code is quite similar to the Room class, but the challenge is deciding which data structure to use. The only difference between the previous example is the inventory size and the amount of data to handle.

Stadiums can have up to 100,000 seats. That’s huge, and using a plain array may not be the best choice anymore.

Possible issue

Jason Statham is a security guard on the stadium backed with Dwayne software, who receives 100 IDs of wanted people from the police. For each ID, he must check all 100,000 seats to see if the person is inside.

Why This Is Problematic:

Time Delay: The guard wastes time checking through the massive array, possibly leading to security bottlenecks. This leads to 10,000,000 checks in total, which is extremely inefficient.
Memory Waste: The array allocates a huge block of contiguous memory, which can occupy RAM and software will stuck.

You see, the code is very similar, and the situations are almost identical — everything’s the same except for the input size. When the data grows, the code slows down, and we need to address this.

Let’s consider a linked list:

It might be better for certain operations, like the “kick” operation because it doesn’t require swapping elements after deletion. However, the linked list comes with a tradeoff — it uses more memory. Due to the nature of having pointers to the next chunk of memory, it can consume a lot of memory — like 10 ^ 5 bytes, or 100KB, just to preserve the structure.

Another option is a hash table:

What if we place our seats in a hash table, instead of using an array or a linked list? Would it introduce memory or time complexity overhead?

The answer to this question lies within the structure of the hash table itself. If we understand how it works, we can see its pros and cons and know when it’s the right choice. This knowledge allows us to compare it with other structures and decide exactly what we need.

Let’s say that — a typical hash table implementation is essentially an array with a smart twist.

How It Works

Imagine an array with many slots. In each slot, you can store some information by default. But in a hash table, we do this more intelligently. We use a hash function for each element that we want to add, update, or delete. This hash function calculates a hash, which is the index of the cell in the array.

The simplest hash function is just taking the remainder when dividing the value by the size of the array:

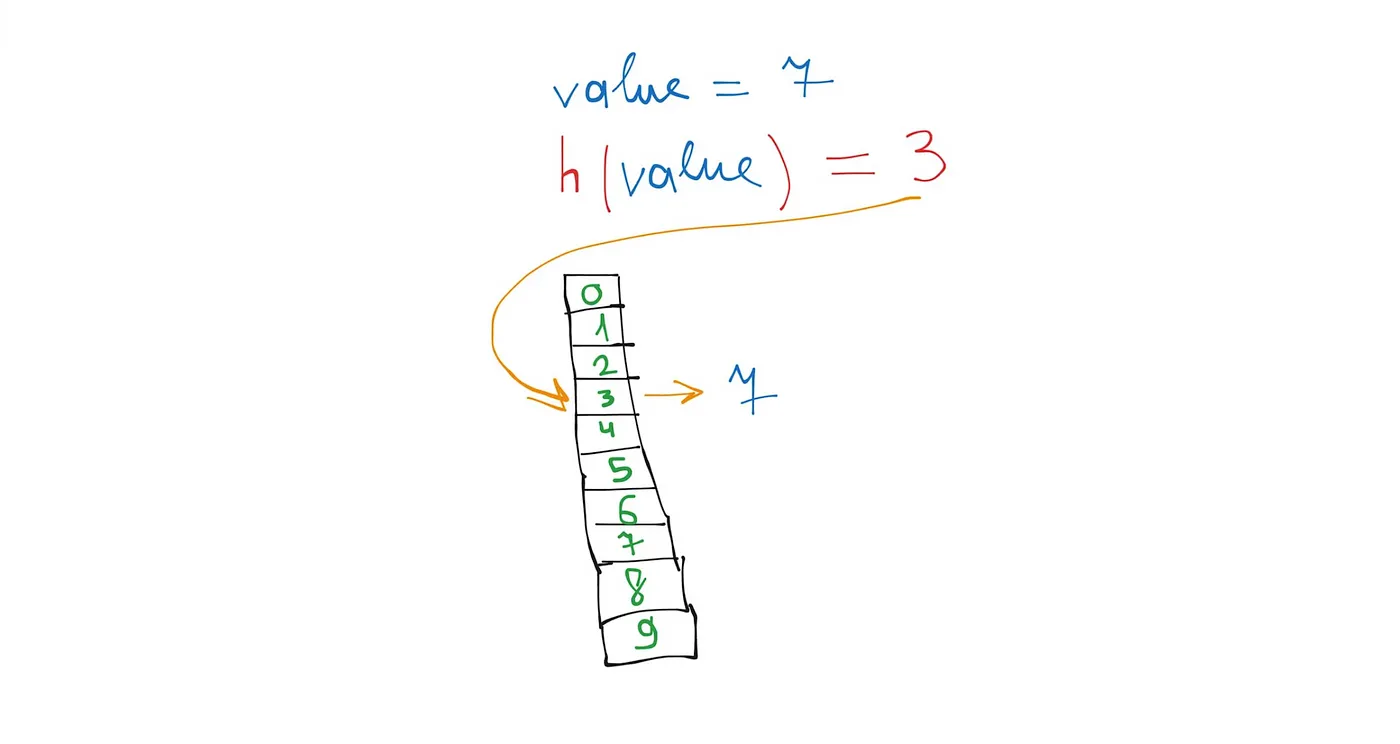
hash = ID % array_size

For example, if I want to add a person with ID 7 to my hash table, I pass this value to the hash function. The function calculates a hash — let’s say it returns 3 — and we place the person with ID 7 in the cell with index 3.

Using this hash, we immediately know that the person with ID 7 is at index 3. The same is going on for search: array[hash(7)]will find our value.

Hash function

Handling Collisions

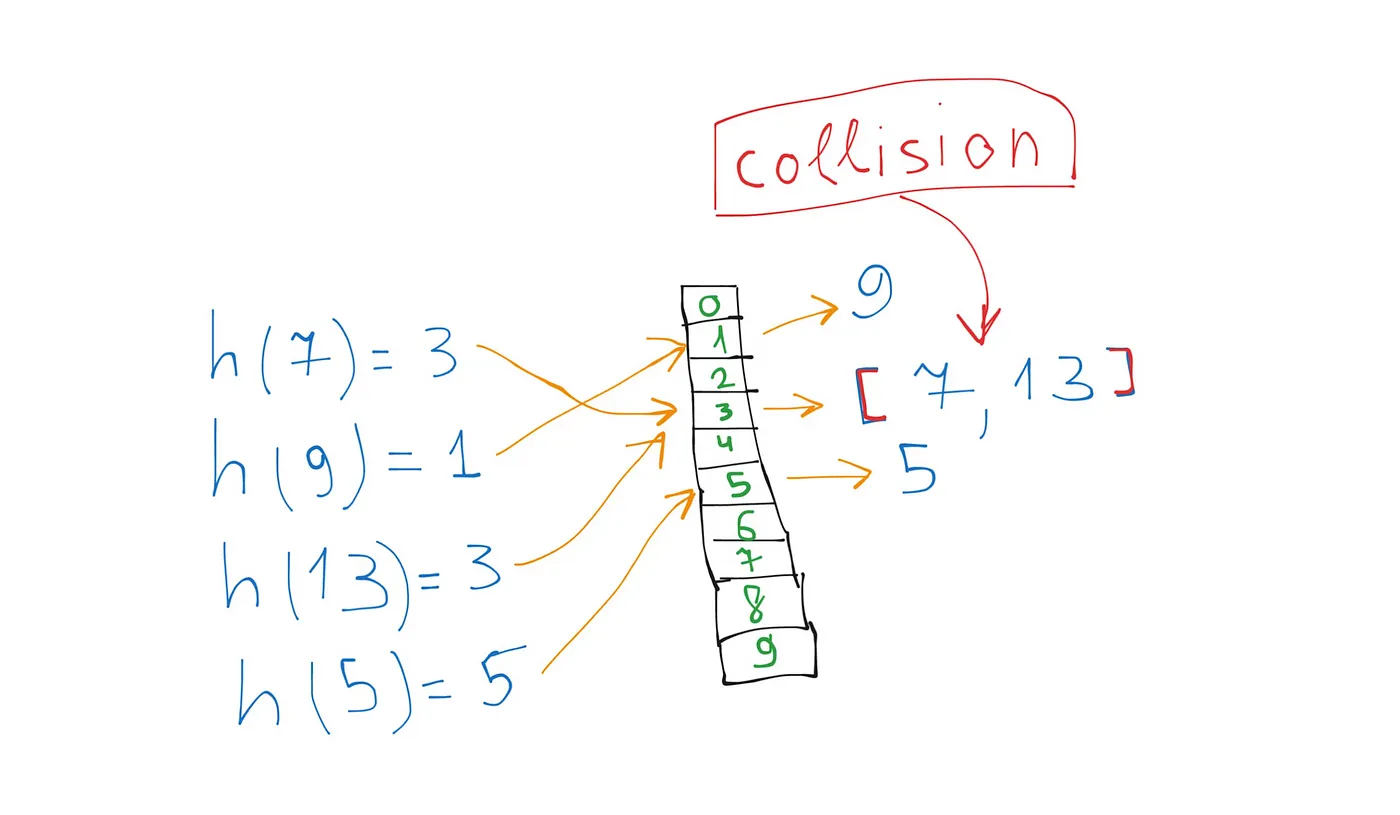
But there’s a problem: sometimes different values can produce the same hash. This happens because we distribute all values in a limited memory location and the plain array values can’t handle all the entries by themselves.

Instead of storing just one value in each cell, we will store an array or linked list of values that share the same hash. Then, when we need to find a value, we simply iterate through this list until we find the right one.

Handle collisions

Importance of a Good Hash Function

As you can see, it’s not exactly magic. If we create a bad hash function that doesn’t distribute our values evenly, we’ll end up with some cells being more crowded than others.

For example, IDs like 7, 17, 27, and so on will all map to the same index (3) with hash = number % 10 (array size).

In this case, the performance will be almost as slow as using a plain array. This is why it’s crucial to choose a good hash function to make sure values are distributed as evenly as possible.

Here you can read more about different types of hash functions: https://www.geeksforgeeks.org/hash-functions-and-list-types-of-hash-functions/ and https://rurban.github.io/smhasher/

Advanced part

Now we know how it works. But maybe you had a question, how does it perform in a constant time and preserve this speed on the full life cycle? We saw that there is no magic under the hood but some smart decisions.

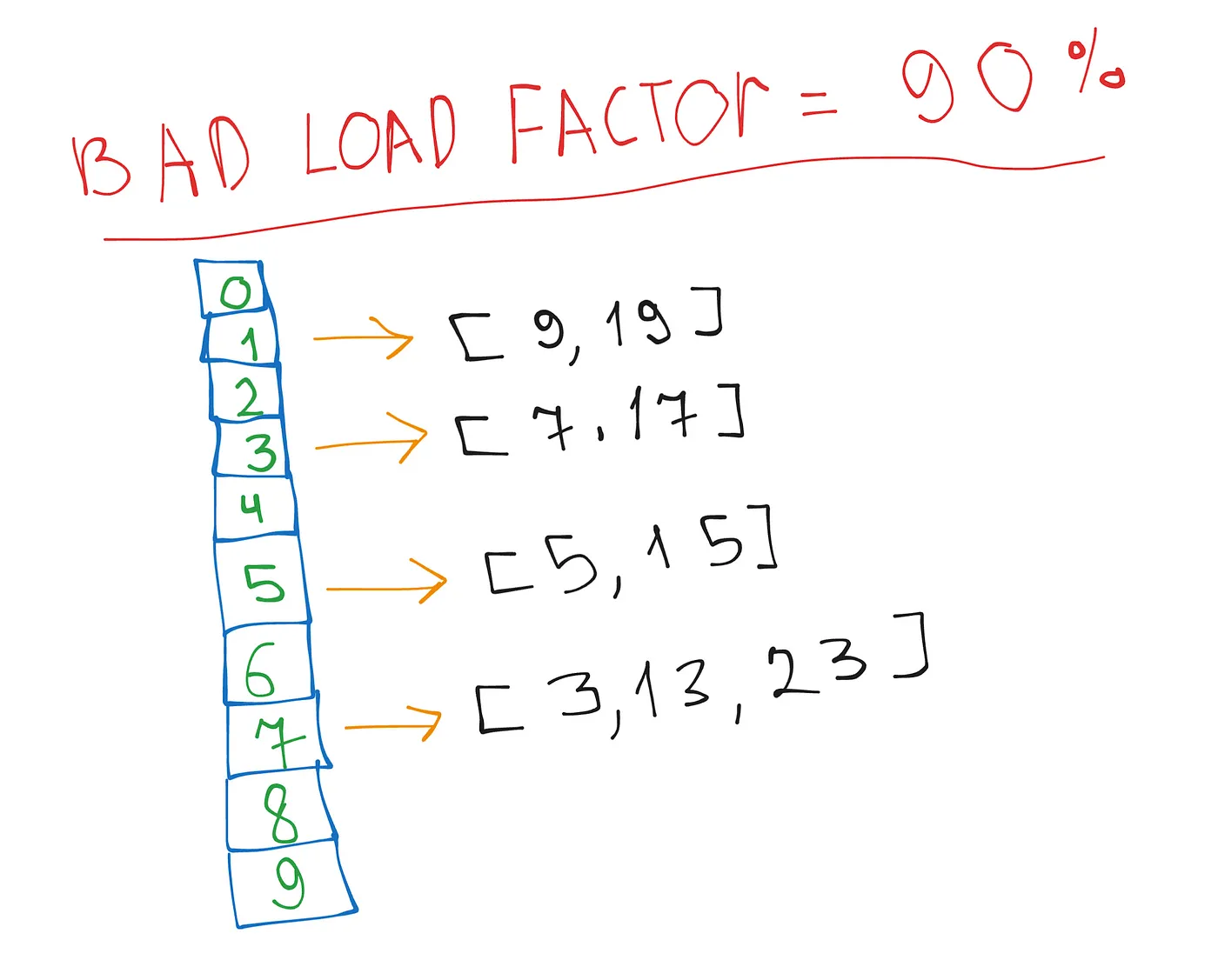
To preserve blazingly fast operations, we need to introduce a new term — load factor. In hash tables, the load factor is the ratio of the number of elements to the size of the array.

A high load factor means more collisions because more elements are placed into fewer slots:

Bad load factor

Vice versa, a low load factor means fewer collisions but more wasted space:

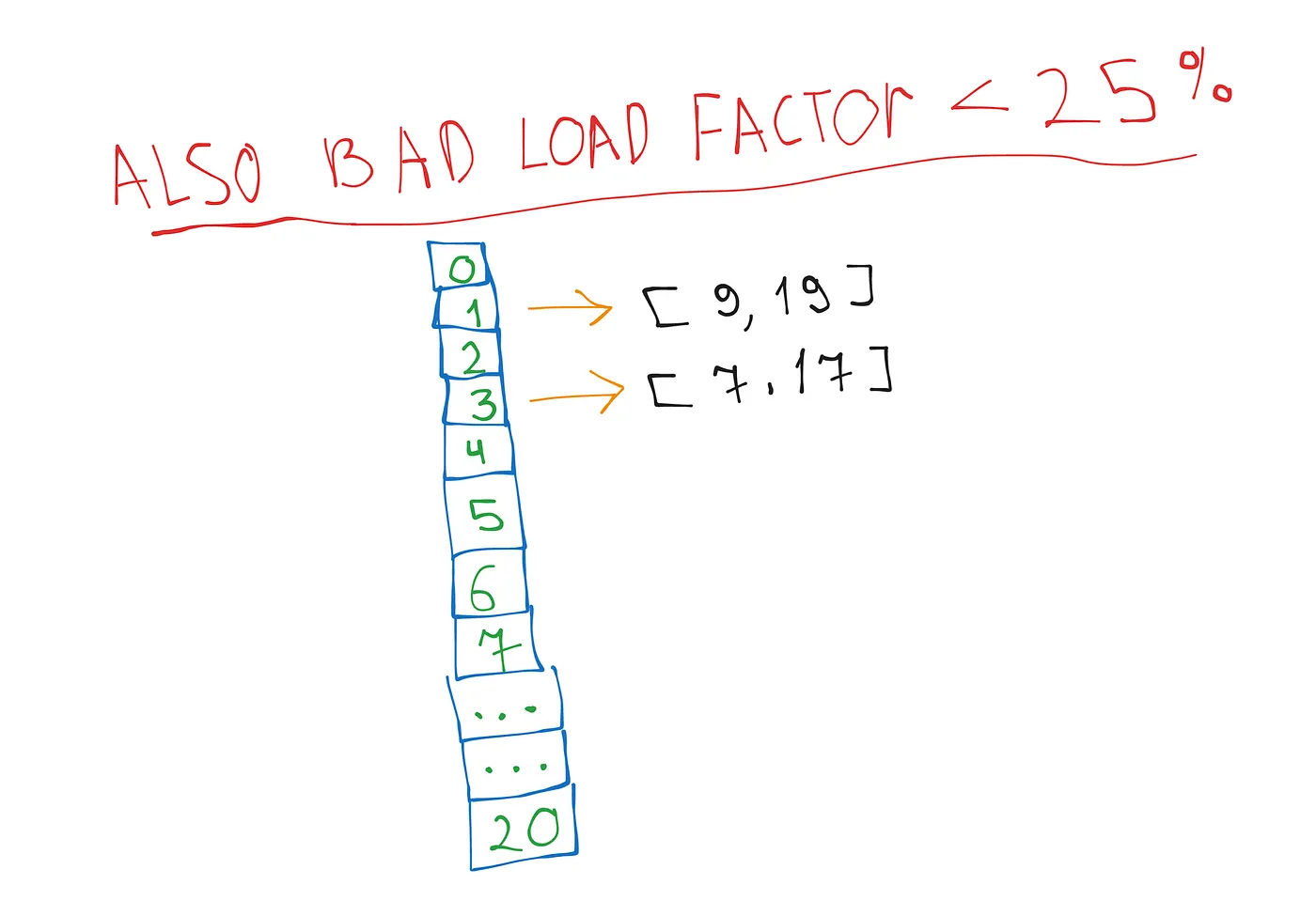
Another bad load factor

To balance this, we need to resize the array when the load factor reaches a certain threshold. A good load factor for hash tables is typically around 0.7 (70%). This gives us a balance between efficient memory usage and maintaining fast search, insertion, and deletion times:

GOOD_LOAD_FACTOR = 0.7
BAD_LOAD_FACTOR = 0.25

If loadFactor > GOOD_LOAD_FACTOR:
  resize(array.size * 2) -> creation of the new, bigger array

If loadFactor < BAD_LOAD_FACTOR:
  resize(array.size // 2) -> creation of the new, smaller array


resize function: recalculates all elements inside of the old hash table 
and put them in the resized one with a new calculated hashes

It is worth mentioning that when we resize a hash table, it costs O(N) operations, which can be expensive. To maintain constant-time operations, we want to avoid resizing too frequently, but we also need to preserve the right load factor to ensure performance.

Implementation

Here is my implementation of a hash table using the method explained above (separate chaining method). For hashing, I am using multiplication by a large prime number for numeric types and the MurmurHash algorithm for other data types:

// Hash function used for hashing string
import { murmur3 } from "murmurhash-js";
// Plain linked list, optimized for insertion
import { LinkedList } from "../linked-lists/sll.js";

// memoize execution of heavy functions as hashing
function memoize(fn) {
  const obj = {};

  return function (arg) {
    if (obj[arg]) {
      return obj[arg];
    } else {
      const res = fn(arg);

      obj[arg] = res;

      return res;
    }
  };
}

function getHashCode(value) {
  if (typeof value === "number") return value * 397;

  const str = JSON.stringify(value);

  return murmur3(str, "seed");
}

const memoizedHash = memoize(getHashCode);

export class HashTable {
  constructor() {
    this._array = Array(this.#MIN_LENGTH);
    this._size = 0;
  }

  get size() {
    return this._size;
  }

  get #MIN_LENGTH() {
    return 5;
  }

  get #LOAD_FACTOR_UPPER_BOUND() {
    return 0.7;
  }

  get #LOAD_FACTOR_LOWER_BOUND() {
    return 0.25;
  }

  #getLoadFactor() {
    return this._size / this._array.length;
  }

  #getHash(value) {
    return memoizedHash(value);
  }

  #resize(arrayLength) {
    if (arrayLength <= this.#MIN_LENGTH) return false;

    const resizedArray = Array(arrayLength);

    for (let i = 0; i < this._array.length; i++) {
      const oldLinkedList = this._array[i];

      if (!oldLinkedList) continue;

      let node = oldLinkedList.head;
      let left = oldLinkedList.size;

      while (left > 0) {
        const hash = this.#getHash(node.value);
        const idx = hash % resizedArray.length;
        const newLinkedList = resizedArray[idx] || new LinkedList();

        newLinkedList.push(node.value);

        resizedArray[idx] = newLinkedList;

        node = node.next;
        left--;
      }
    }

    this._array = resizedArray;
  }

  #resizeIfNeeded() {
    const loadFactor = this.#getLoadFactor();

    if (loadFactor > this.#LOAD_FACTOR_UPPER_BOUND) {
      const newLength = this._array.length * 2;
      this.#resize(newLength);
    }

    if (loadFactor < this.#LOAD_FACTOR_LOWER_BOUND) {
      const newLength = Math.floor(this._array.length / 2);
      this.#resize(newLength);
    }
  }

  insert(value) {
    this.#resizeIfNeeded();

    const hash = this.#getHash(value);
    const idx = hash % this._array.length;

    if (!this._array[idx]) {
      this._array[idx] = new LinkedList();
    }

    const linkedList = this._array[idx];

    linkedList.push(value);

    this._size++;

    return true;
  }

  has(value) {
    const hash = this.#getHash(value);
    const idx = hash % this._array.length;

    if (!this._array[idx]) return false;

    const linkedList = this._array[idx];

    return !!linkedList.find(value);
  }

  remove(value) {
    if (!this.has(value)) return false;

    const hash = this.#getHash(value);
    const idx = hash % this._array.length;
    const linkedList = this._array[idx];

    linkedList.remove(value);
    this._size--;

    return true;
  }
}

Performance

Here is a comparison of insert, search, and remove operations on 100,000 elements for a linked list, array, map (built-in hash table implementation), and a custom hash table written above:

P.S. We nearly caught up with the native JS hash table implementation :)

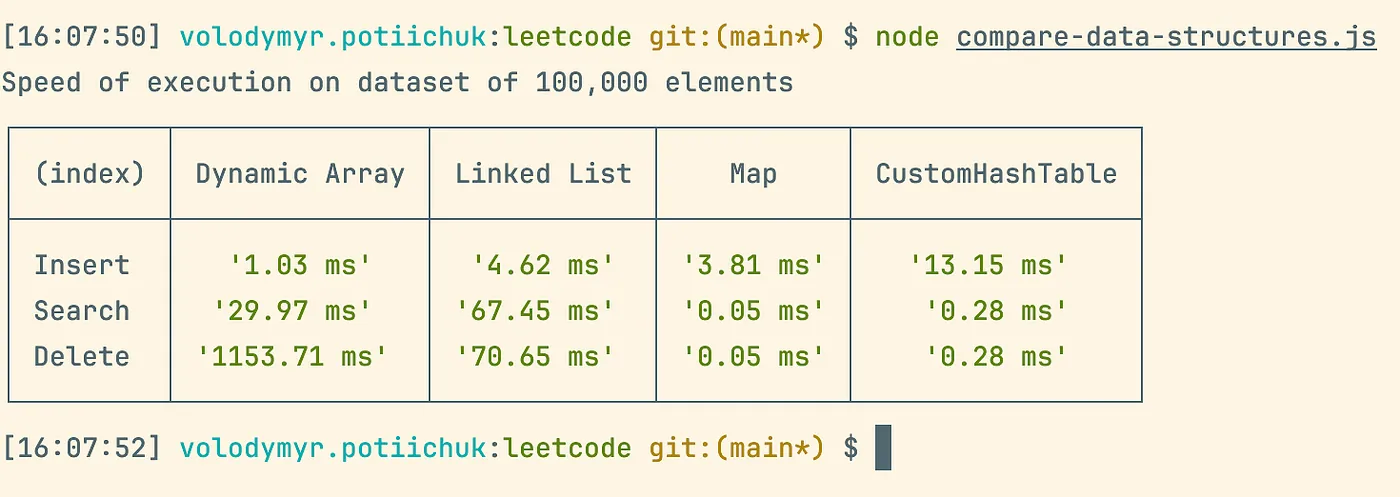
Comparsion of data structures

And, as you can see, there’s a noticeable difference in execution speed between these data structures when handling large datasets.

For example, if you need to frequently search or delete values in your data structure, but rarely insert it, a hash table would be a great idea (as our stadium). But if you need to insert often, and rarely search or maybe your data size is tiny — I would think about an array or linked list.

You can check the full comparison file and related files on my GitHub repo: https://github.com/ExuCounter/algorithms-and-data-structures

That’s it! I hope you enjoyed it. Don’t forget to like and subscribe for more articles.

How hash tables outperform other data structures

Imagine such story

Another story

How It Works

Handling Collisions

Importance of a Good Hash Function

Advanced part

Implementation

Performance

Previous and next article

Creation of a job processing library using Elixir and Redis

Build LMS platform from scratch. Part 1 — define requirements.

Subscribe to my newsletter